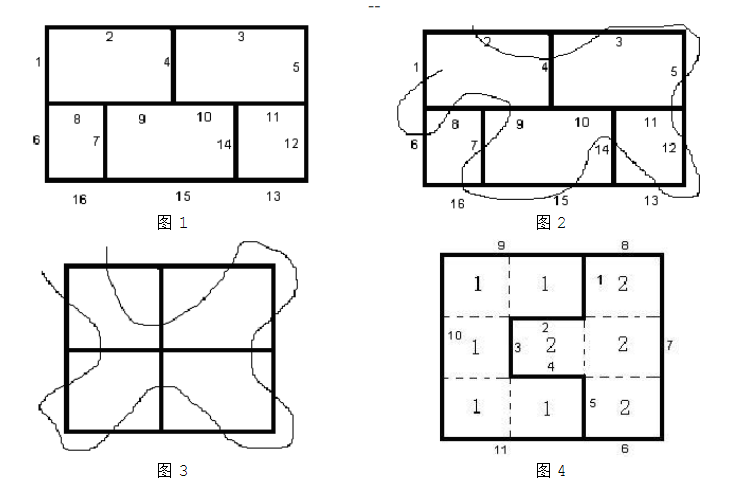
一个同学给了我一个逻辑游戏。他给了我图 $1$ ,在这个图上,每一段边界都已经进行了编号。我的任务是在图中画一条连续的曲线,使得这条曲线穿过每一个边界一次且仅穿过一次,而且曲线的起点和终点都在这整个区域的外面。这条曲线是允许自交的。 对于图 $1$ ,我的同学告诉我画出这样的一条曲线(图 $2$)是不可能的,但是对于有的图形(比如图 $3$ ),画出这样一条曲线是可行的。对于给定的一个图,我想知道是否可以画出满足要求的曲线。
输入:
输入的图形用一个 $n * n$ 的矩阵表示的。矩阵的每一个单元里有一个 $0$ 到 $255$ 之间(包括和 )的整数。处于同一个区域的单元里的数相同,相邻区域的数不同(但是不相邻的区域里的数可能相同)。 输入的第一行是 $n(0 < n < 100)$ 。以下的 $n$ 行每行包括 $n$ 个整数,分别给出对应的单元里的整数(这 $n$ 个整数之间用空格分开)。图 $4$ 给出了输入样例对应的图形。
输出: 当可以画出满足题意的曲线的时候,输出 `YES` ;否则,输出 `NO` 。
输入样例:
```
3
1 1 2
1 2 2
1 1 2
```
输出样例:
```
YES
```
提示:plimba 函数求解的是对于一个同色块,它的边缘有多少条边。
#include <stdio.h>
#include <math.h>
int orig, n, ns, a[102][102], bun;
int d[] = {1, 0, -1, 0, 0, 1, 0, -1 };
void plimba(int x, int y) {
int i, xx, yy;
a[x][y] = -a[x][y];
if (abs(a[x - 1][y]) != orig && (___(1)___ != a[x - 1][y]
|| abs(a[x][y - 1]) != orig)) ns++;
if (abs(a[x + 1][y]) != orig && (a[x + 1][y - 1] != a[x + 1][y]
|| abs(a[x][y - 1]) != orig)) ns++;
if (abs(a[x][y - 1]) != orig && (___(2)___ != a[x][y - 1]
|| abs(a[x - 1][y]) != orig)) ns++;
if (abs(a[x][y + 1]) != orig && (a[x - 1][y + 1] != a[x][y + 1]
|| abs(a[x - 1][y]) != orig)) ns++;
for (i = 0; i < 4; i++) {
xx = x + d[2 * i];
yy = y + ___(3)___;
if (xx >= 1 && xx <= n && yy >= 1
&& yy <= n && ___(4)___) plimba(xx, yy);
}
}
int main() {
int i, j;
bun = 1;
scanf("%d", & n);
for (i = 0; i <= n + 1; i++)
for (j = 0; j <= n + 1; j++) a[i][j] = 0;
a[0][0] = -1;
a[n + 1][0] = -1;
a[0][n + 1] = -1;
a[n + 1][n + 1] = -1;
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++) scanf("%d", & a[i][j]);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++) {
if (a[i][j] > -1) {
ns = 0;
___(5)___;
plimba(i, j);
if (ns % 2 == 1) bun = 0;
}
}
if (bun) printf("YES\n");
else printf("NO\n");
return 0;
}
1. C。
2. D。
3. A。
4. D。
5. D。
可以看出,因为我们要从外部进入,然后从外部离开,所以对于任何一个区域,其必须与外部或其他区域有着偶数个边界,这样才可以有进有出,否则就无解,这与我们的欧拉回路是很相似的。所以我们的做法就比较简单了,我们可以分别判断每个区域,如果这个区域有奇数条分界线就答案无解,输出 `NO` 。否则如果所有区域都有偶数条分界线,那么就一定存在至少一种解,输出 `YES` 即可。在这段代码中通过 `a[i][j]` 的正负来标识了已到达的区域和未到达的区域。在每次的 `plimba` 中搜索该区域所有的边界线并储存到 `ns` 中,对 `ns` 进行判断来判断是否有解。至于对边界线的判断有四种情况,即代码当中 `plimba` 函数内对应的四种情况,如果对这四种情况不是很清楚,可以画出矩阵来尝试模拟一下。