CSP-J1入门级初赛试卷[2023]

第1题

在C++中，下面哪个关键字用于声明一个变量，其值不能被修改？（）。

unsigned

const

static

mutable

共 2 分　

第2题

八进制数12345670 和07654321的和为（）。

22222221

21111111

22111111

22222211

共 2 分　

第3题

阅读下述代码，请问修改data的value成员以存储3.14，正确的方式是（）。

union Data{
int num;
float value;
char symbol;
};
union Data data;

data.value = 3.14;

value.data = 3.14;

data->value = 3.14;

value->data = 3.14;

共 2 分　

第4题

假设有一个链表的节点定义如下：

struct Node {
int data;
Node* next;
};

现在有一个指向链表头部的指针：Node* head。如果想要在链表中插入一个新节点，其成员data的值为42，并使新节点成为链表的第一个节点，下面哪个操作是正确的？（）

Node* newNode = new Node; newNode->data = 42; newNode->next = head; head = newNode;

Node* newNode = new Node; head->data = 42; newNode->next = head; head = newNode;

Node* newNode = new Node; newNode->data = 42; head->next = newNode;

Node* newNode = new Node; newNode->data = 42; newNode->next = head;

共 2 分　

第5题

根节点的高度为1，一根拥有2023个节点的三叉树高度至少为（）。

共 2 分　

第6题

小明在某一天中依次有七个空闲时间段，他想要选出至少一个空闲时间段来练习唱歌，但他希望任意两个练习的时间段之间都有至少两个空闲的时间段让他休息，则小明一共有（）种选择时间段的方案。

共 2 分　

第7题

以下关于高精度运算的说法错误的是（）。

高精度计算主要是用来处理大整数或需要保留多位小数的运算。

大整数除以小整数的处理的步骤可以是，将被除数和除数对齐，从左到右逐位尝试将除数乘以某个数，通过减法得到新的被除数，并累加商。

高精度乘法的运算时间只与参与运算的两个整数中长度较长者的位数有关。

高精度加法运算的关键在于逐位相加并处理进位。

共 2 分　

第8题

后缀表达式“6 2 3 + - 3 8 2 / + * 2 ^ 3 +”对应的中缀表达式是（）

((6 - (2 + 3)) * (3 + 8 / 2)) ^ 2 + 3

6 - 2 + 3 * 3 + 8 / 2 ^ 2 + 3

(6 - (2 + 3)) * ((3 + 8 / 2) ^ 2) + 3

6 - ((2 + 3) * (3 + 8 / 2)) ^ 2 + 3

共 2 分　

第9题

数(101010)2和(166)8的和为（）。

(10110000)2

(236)8

(158)10

(A0)16

共 2 分　

第10题

假设有一组字符{a,b,c,d,e,f}，对应的频率分别为5%，9%，12%，13%，16%，45%。请问以下哪个选项是字符a,b,c,d,e,f分别对应的一组哈夫曼编码？（）

1111，1110，101，100，110，0

1010，1001，1000，011，010，00

000，001，010，011，10，11

1010，1011，110，111，00，01

共 2 分　

第11题

给定一棵二叉树，其前序遍历结果为：ABDECFG，中序遍历结果为：DEBACFG。请问这棵树的正确后序遍历结果是什么？（）

EDBFGCA

EDBGCFA

DEBGFCA

DBEGFCA

共 2 分　

第12题

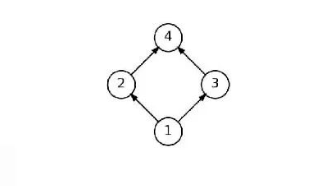
考虑一个有向无环图，该图包括4条有向边：(1,2)，(1,3)，(2,4)，和(3,4)。以下哪个选项是这个有向无环图的一个有效的拓扑排序？（）

有向无环图

4，2，3，1

1，2，3，4

1，2，4，3

2，1，3，4

共 2 分　

第13题

在计算机中，以下哪个选项描述的数据存储容量最小？（）

字节（byte）

比特（bit）

字（word）

千字节（kilobyte）

共 2 分　

第14题

一个班级有10个男生和12个女生。如果要选出一个3人的小组，并且小组中必须至少包含1个女生，那么有多少种可能的组合？（）

共 2 分　

第15题

以下哪个不是操作系统？（）

Linux

Windows

Android

HTML

共 2 分　

第16题

#include<iostream>
#include<cmath>
using namespace std;
double f(double a,double b,double c){
 double s=(a+b+c)/2;
 return sqrt(s*(s-a)*(s-b)*(s-c));
}
int main(){
 cout.flags(ios::fixed);
 cout.precision(4);
 
int a,b,c;
 cin>>a>>b>>c;
 cout<<f(a,b,c)<<endl;
 return 0;
}

假设输入的所有数都为不超过1000的正整数，完成下面的判断题和单选题：

当输入为“2 2 2”时，输出为“1.7321”（）

正确

错误

共 2 分　

第17题

#include<iostream>
#include<cmath>
using namespace std;
double f(double a,double b,double c){
 double s=(a+b+c)/2;
 return sqrt(s*(s-a)*(s-b)*(s-c));
}
int main(){
 cout.flags(ios::fixed);
 cout.precision(4);
 
int a,b,c;
 cin>>a>>b>>c;
 cout<<f(a,b,c)<<endl;
 return 0;
}

假设输入的所有数都为不超过1000的正整数，完成下面的判断题和单选题：

将第7行中的"（s-b）*（s-c）"改为"（s-c）*（s-b）"不会影响程序运行的结果（）

正确

错误

共 2 分　

第18题

#include<iostream>
#include<cmath>
using namespace std;
double f(double a,double b,double c){
 double s=(a+b+c)/2;
 return sqrt(s*(s-a)*(s-b)*(s-c));
}
int main(){
 cout.flags(ios::fixed);
 cout.precision(4);
 
int a,b,c;
 cin>>a>>b>>c;
 cout<<f(a,b,c)<<endl;
 return 0;
}

假设输入的所有数都为不超过1000的正整数，完成下面的判断题和单选题：

程序总是输出四位小数（）

正确

错误

共 2 分　

第19题

#include<iostream>
#include<cmath>
using namespace std;
double f(double a,double b,double c){
 double s=(a+b+c)/2;
 return sqrt(s*(s-a)*(s-b)*(s-c));
}
int main(){
 cout.flags(ios::fixed);
 cout.precision(4);
 
int a,b,c;
 cin>>a>>b>>c;
 cout<<f(a,b,c)<<endl;
 return 0;
}

假设输入的所有数都为不超过1000的正整数，完成下面的判断题和单选题：

当输入为“3 4 5”时，输出为（）

"6.0000"

"12.0000"

"24.0000"

"30.0000"

共 2 分　

第20题

#include<iostream>
#include<cmath>
using namespace std;
double f(double a,double b,double c){
 double s=(a+b+c)/2;
 return sqrt(s*(s-a)*(s-b)*(s-c));
}
int main(){
 cout.flags(ios::fixed);
 cout.precision(4);
 
int a,b,c;
 cin>>a>>b>>c;
 cout<<f(a,b,c)<<endl;
 return 0;
}

假设输入的所有数都为不超过1000的正整数，完成下面的判断题和单选题：

当输入为“5 12 13”时，输出为（）

"24.0000"

"30.0000"

"60.0000"

"120.0000"

共 2 分　

第21题

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int f(string x,string y){
 int m=x.size();
 int n=y.size();
 vector<vector<int>> v(m+1,vector<int>(n+1,0));
 for(int i=1;i<=m;i++){
 for(int j=1;j<=n;j++){
 if(x[i-1]==y[j-1]){
 v[i][j]=v[i-1][j-1]+1;
 }else{
 v[i][j]=max(v[i-1][j],v[i][j-1]);
 }
 }
 }
 return v[m][n];
 }

 bool g(string x,string y){
 if(x.size() != y.size()){
 return false;
 }
 return f(x+x,y)==y.size();
 }
 int main(){
 string x,y;
 cin>>x>>y;
 cout<<g(x,y)<<endl;
 return 0;
}

f函数的返回值小于等于min（n,m）。（）

正确

错误

共 2 分　

第22题

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int f(string x,string y){
 int m=x.size();
 int n=y.size();
 vector<vector<int>> v(m+1,vector<int>(n+1,0));
 for(int i=1;i<=m;i++){
 for(int j=1;j<=n;j++){
 if(x[i-1]==y[j-1]){
 v[i][j]=v[i-1][j-1]+1;
 }else{
 v[i][j]=max(v[i-1][j],v[i][j-1]);
 }
 }
 }
 return v[m][n];
 }
 bool g(string x,string y){
 if(x.size() != y.size()){
 return false;
 }
 return f(x+x,y)==y.size();
 }
 int main(){
 string x,y;
 cin>>x>>y;
 cout<<g(x,y)<<endl;
 return 0;
}

f函数的返回值等于两个输入字符串的最长公共子串的长度。（）

正确

错误

共 2 分　

第23题

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int f(string x,string y){
 int m=x.size();
 int n=y.size();
 vector<vector<int>> v(m+1,vector<int>(n+1,0));
 for(int i=1;i<=m;i++){
 for(int j=1;j<=n;j++){
 if(x[i-1]==y[j-1]){
 v[i][j]=v[i-1][j-1]+1;
 }else{
 v[i][j]=max(v[i-1][j],v[i][j-1]);
 }
 }
 }
 return v[m][n];
 }
 bool g(string x,string y){
 if(x.size() != y.size()){
 return false;
 }
 return f(x+x,y)==y.size();
 }
 int main(){
 string x,y;
 cin>>x>>y;
 cout<<g(x,y)<<endl;
 return 0;
}

当输入两个完全相同的字符串时，g函数的返回值总是true。（）

正确

错误

共 2 分　

第24题

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int f(string x,string y){
 int m=x.size();
 int n=y.size();
 vector<vector<int>> v(m+1,vector<int>(n+1,0));
 for(int i=1;i<=m;i++){
 for(int j=1;j<=n;j++){
 if(x[i-1]==y[j-1]){
 v[i][j]=v[i-1][j-1]+1;
 }else{
 v[i][j]=max(v[i-1][j],v[i][j-1]);
 }
 }
 }
 return v[m][n];
 }
 bool g(string x,string y){
 if(x.size() != y.size()){
 return false;
 }
 return f(x+x,y)==y.size();
 }
 int main(){
 string x,y;
 cin>>x>>y;
 cout<<g(x,y)<<endl;
 return 0;
}

将第19行中的“v[m][n]”替换为“v[n][m]”，那么该程序（）

行为不变

只会改变输出

一定非正常退出

可能非正常退出

共 2 分　

第25题

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int f(string x,string y){
 int m=x.size();
 int n=y.size();
 vector<vector<int>> v(m+1,vector<int>(n+1,0));
 for(int i=1;i<=m;i++){
 for(int j=1;j<=n;j++){
 if(x[i-1]==y[j-1]){
 v[i][j]=v[i-1][j-1]+1;
 }else{
 v[i][j]=max(v[i-1][j],v[i][j-1]);
 }
 }
 }
 return v[m][n];
 }
 bool g(string x,string y){
 if(x.size() != y.size()){
 return false;
 }
 return f(x+x,y)==y.size();
 }
 int main(){
 string x,y;
 cin>>x>>y;
 cout<<g(x,y)<<endl;
 return 0;
}

当输入为 "csp-j p-jcs" 时,输出为( )

“0”

“1”

“T”

“F”

共 2 分　

第26题

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int f(string x,string y){
 int m=x.size();
 int n=y.size();
 vector<vector<int>> v(m+1,vector<int>(n+1,0));
 for(int i=1;i<=m;i++){
 for(int j=1;j<=n;j++){
 if(x[i-1]==y[j-1]){
 v[i][j]=v[i-1][j-1]+1;
 }else{
 v[i][j]=max(v[i-1][j],v[i][j-1]);
 }
 }
 }
 return v[m][n];
 }
 bool g(string x,string y){
 if(x.size() != y.size()){
 return false;
 }
 return f(x+x,y)==y.size();
 }
 int main(){
 string x,y;
 cin>>x>>y;
 cout<<g(x,y)<<endl;
 return 0;
}

当输入为“csppsc spsccp”时，输出为：（）

“T”

“F”

“0”

“1”

共 2 分　

第27题

#include <iostream>
#include <cmath>
using namespace std;
int solve1(int n){
return n*n;
}
int solve2(int n){
 int sum=0;
 for(int i=1;i<=sqrt(n);i++){
 if(n%i==0){
 if(n/i==i){
 sum+=i*i;
 }else{
 sum+=i*i+(n/i)*(n/i);
 }
 }
}
 return sum;
}
int main(){
 int n;
 cin>>n;
 cout<<solve2(solve1(n))<<" "<<solve1((solve2(n)))<<endl;
 return 0;
}

假设输入的n是绝对值不超过1000的整数，完成下面的判断题和单选题:

如果输入的n为正整数，solve2函数的作用是计算n所有的因子的平方和（）

正确

错误

共 3 分　

第28题

#include <iostream>
#include <cmath>
using namespace std;
int solve1(int n){
return n*n;
}
int solve2(int n){
 int sum=0;
 for(int i=1;i<=sqrt(n);i++){
 if(n%i==0){
 if(n/i==i){
 sum+=i*i;
 }else{
 sum+=i*i+(n/i)*(n/i);
 }
 }
}
 return sum;
}
int main(){
 int n;
 cin>>n;
 cout<<solve2(solve1(n))<<" "<<solve1((solve2(n)))<<endl;
 return 0;
}

假设输入的n是绝对值不超过1000的整数，完成下面的判断题和单选题:

第13~14行的作用是避免n的平方根因子i（或n/i）进入第16行而被计算两次（）

正确

错误

共 3 分　

第29题

#include <iostream>
#include <cmath>
using namespace std;
int solve1(int n){
return n*n;
}
int solve2(int n){
int sum=0;
for(int i=1;i<=sqrt(n);i++){
if(n%i==0){
if(n/i==i){
sum+=i*i;
}else{
sum+=i*i+(n/i)*(n/i);
}
}
}
return sum;
}
int main(){
int n;
cin>>n;
cout<<solve2(solve1(n))<<" "<<solve1((solve2(n)))<<endl;
return 0;
}

假设输入的n是绝对值不超过1000的整数，完成下面的判断题和单选题:

如果输入的n为质数，solve2（n）的返回值为n²+1（）

正确

错误

共 3 分　

第30题

#include <iostream>
#include <cmath>
using namespace std;
int solve1(int n){
return n*n;
}
int solve2(int n){
int sum=0;
for(int i=1;i<=sqrt(n);i++){
if(n%i==0){
if(n/i==i){
sum+=i*i;
}else{
sum+=i*i+(n/i)*(n/i);
}
}
}
return sum;
}
int main(){
int n;
cin>>n;
cout<<solve2(solve1(n))<<" "<<solve1((solve2(n)))<<endl;
return 0;
}

假设输入的n是绝对值不超过1000的整数，完成下面的判断题和单选题:

如果输入的n为质数p的平方，那么solve2（n）的返回值为（）

p²+p+1

n²+n+1

n²+1

p4+2p²+1

共 3 分　

第31题

#include <iostream>
#include <cmath>
using namespace std;
int solve1(int n){
return n*n;
}
int solve2(int n){
int sum=0;
for(int i=1;i<=sqrt(n);i++){
if(n%i==0){
if(n/i==i){
sum+=i*i;
}else{
sum+=i*i+(n/i)*(n/i);
}
}
}
return sum;
}
int main(){
int n;
cin>>n;
cout<<solve2(solve1(n))<<" "<<solve1((solve2(n)))<<endl;
return 0;
}

假设输入的n是绝对值不超过1000的整数，完成下面的判断题和单选题:

当输入为正整数时，第一项减去第二项的差值一定（）

大于0

大于等于0 且不一定大于0

小于0

小于等于0 且不一定小于0

共 3 分　

第32题

#include <iostream>
#include <cmath>
using namespace std;
int solve1(int n){
return n*n;
}
int solve2(int n){
int sum=0;
for(int i=1;i<=sqrt(n);i++){
if(n%i==0){
if(n/i==i){
sum+=i*i;
}else{
sum+=i*i+(n/i)*(n/i);
}
}
}
return sum;
}
int main(){
int n;
cin>>n;
cout<<solve2(solve1(n))<<" "<<solve1((solve2(n)))<<endl;
return 0;
}

假设输入的n是绝对值不超过1000的整数，完成下面的判断题和单选题:

当输入为“5”时，输出为（）

"651.625"

"650.729"

"651.676"

"652.625"

共 3 分　

第33题

（寻找被移除的元素）问题，原有长度为n+1,公差为1的等差升序数列，将序列输入到程序的数组时移除了一个元素，导致长度为n的升序数组可能不再连续，除非被移除的是第一个或最后一个元素。需要在数组不连续时，找出被移除的元素。

#include <iostream>
#include <vector>
using namespace std;
int find_missing(vector<int>& nums){
 int left=0,right=nums.size()-1;
 while(left<right){
 int mid=left+(right-left)/2;
 if(nums[mid]==mid+①){
 ②;
 }else{
 ③;
  }
 }
 return ④;
}
int main(){
 int n;
 cin>>n;
 vector<int> nums(n);
 for(int i=0;i<n;i++) cin>>nums[i];
 int misssing_number=find_missing(nums);
 if(missing_number==⑤){
 cout<<"Sequence is consecutive"<<endl;
 }else{
 cout<<"Missing numbers is"<<missing_number<<endl;
 }
return 0;
}

①处应填（）

nums[0]

right

left

共 3 分　

第34题

#include <iostream>
#include <vector>
using namespace std;
int find_missing(vector<int>& nums){
 int left=0,right=nums.size()-1;
 while(left<right){
 int mid=left+(right-left)/2;
 if(nums[mid]==mid+①){
 ②;
 }else{
 ③;
  }
 }
 return ④;
}
int main(){
 int n;
 cin>>n;
 vector<int> nums(n);
 for(int i=0;i<n;i++) cin>>nums[i];
 int misssing_number=find_missing(nums);
 if(missing_number==⑤){
 cout<<"Sequence is consecutive"<<endl;
 }else{
 cout<<"Missing numbers is"<<missing_number<<endl;
 }
return 0;
}

②处应填（）

left=mid+1

right=mid-1

right=mid

left=mid

共 3 分　

第35题

#include <iostream>
#include <vector>
using namespace std;
int find_missing(vector<int>& nums){
 int left=0,right=nums.size()-1;
 while(left<right){
 int mid=left+(right-left)/2;
 if(nums[mid]==mid+①){
 ②;
 }else{
 ③;
  }
 }
 return ④;
}
int main(){
 int n;
 cin>>n;
 vector<int> nums(n);
 for(int i=0;i<n;i++) cin>>nums[i];
 int misssing_number=find_missing(nums);
 if(missing_number==⑤){
 cout<<"Sequence is consecutive"<<endl;
 }else{
 cout<<"Missing numbers is"<<missing_number<<endl;
 }
return 0;
}

③处应填（）

left=mid+1

right=mid-1

right=mid

left=mid

共 3 分　

第36题

#include <iostream>
#include <vector>
using namespace std;
int find_missing(vector<int>& nums){
 int left=0,right=nums.size()-1;
 while(left<right){
 int mid=left+(right-left)/2;
 if(nums[mid]==mid+①){
 ②;
 }else{
 ③;
  }
 }
 return ④;
}
int main(){
 int n;
 cin>>n;
 vector<int> nums(n);
 for(int i=0;i<n;i++) cin>>nums[i];
 int misssing_number=find_missing(nums);
 if(missing_number==⑤){
 cout<<"Sequence is consecutive"<<endl;
 }else{
 cout<<"Missing numbers is"<<missing_number<<endl;
 }
return 0;
}

④处应填（）

left+nums[0]

right+nums[0]

mid+nums[0]

right+1

共 3 分　

第37题

#include <iostream>
#include <vector>
using namespace std;
int find_missing(vector<int>& nums){
 int left=0,right=nums.size()-1;
 while(left<right){
 int mid=left+(right-left)/2;
 if(nums[mid]==mid+①){
 ②;
 }else{
 ③;
  }
 }
 return ④;
}
int main(){
 int n;
 cin>>n;
 vector<int> nums(n);
 for(int i=0;i<n;i++) cin>>nums[i];
 int misssing_number=find_missing(nums);
 if(missing_number==⑤){
 cout<<"Sequence is consecutive"<<endl;
 }else{
 cout<<"Missing numbers is"<<missing_number<<endl;
 }
return 0;
}

⑤处应填（）

nums[0]+n

nums[0]+n-1

nums[0]+n+1

nums[n-1]

共 3 分　

第38题

（编辑距离）给定两个字符串，每次操作可以选择删除（Delete）、插入（Insert）、替换（Replace），一个字符，求将第一个字符串转换为第二个字符串所需要的最少操作次数。

#include <iostream>
#include <string>
#include <vector>
using namespace std;
int min(int x,int y,int z){
 return min(min(x,y),z);
}
int edit_dist_dp(string str1,string str2){
 int m=str1.length();
 int n=str2.length();
 vector<vector<int>> dp(m+1,vector<int>(n+1));
 for(int i=0;i<=m;i++){
 for(int j=0;j<=n;j++){
 if(i==0)
 dp[i][j]=(1);
 else if(j==0)
 dp[i][j]=(2);
 else if((3))
 dp[i][j]=(4);
 else
 dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],(5));
 }
 }
 return dp[m][n];
}
int main(){
 string str1,str2;
 cin>>str1>>str2;
 cout<<"Mininum number of operation:"
 <<edit_dist_dp(str1,str2)<<endl;
 return 0;
}

①处应填（）

共 3 分　

第39题

#include <iostream>
#include <string>
#include <vector>
using namespace std;
int min(int x,int y,int z){
 return min(min(x,y),z);
}
int edit_dist_dp(string str1,string str2){
 int m=str1.length();
 int n=str2.length();
 vector<vector<int>> dp(m+1,vector<int>(n+1));
 for(int i=0;i<=m;i++){
 for(int j=0;j<=n;j++){
 if(i==0)
 dp[i][j]=(1);
 else if(j==0)
 dp[i][j]=(2);
 else if((3))
 dp[i][j]=(4);
 else
 dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],(5));
 }
 }
 return dp[m][n];
}
int main(){
 string str1,str2;
 cin>>str1>>str2;
 cout<<"Mininum number of operation:"
 <<edit_dist_dp(str1,str2)<<endl;
 return 0;
}

②处应填（）

共 3 分　

第40题

#include <iostream>
#include <string>
#include <vector>
using namespace std;
int min(int x,int y,int z){
 return min(min(x,y),z);
}
int edit_dist_dp(string str1,string str2){
 int m=str1.length();
 int n=str2.length();
 vector<vector<int>> dp(m+1,vector<int>(n+1));
 for(int i=0;i<=m;i++){
 for(int j=0;j<=n;j++){
 if(i==0)
 dp[i][j]=(1);
 else if(j==0)
 dp[i][j]=(2);
 else if((3))
 dp[i][j]=(4);
 else
 dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],(5));
 }
 }
 return dp[m][n];
}
int main(){
 string str1,str2;
 cin>>str1>>str2;
 cout<<"Mininum number of operation:"
 <<edit_dist_dp(str1,str2)<<endl;
 return 0;
}

③处应填（）

str1[i-1]==str2[j-1]

str1[i]==str2[j]

str1[i-1]!=str2[j-1]

str1[i]!=str2[j]

共 3 分　

第41题

#include <iostream>
#include <string>
#include <vector>
using namespace std;
int min(int x,int y,int z){
 return min(min(x,y),z);
}
int edit_dist_dp(string str1,string str2){
 int m=str1.length();
 int n=str2.length();
 vector<vector<int>> dp(m+1,vector<int>(n+1));
 for(int i=0;i<=m;i++){
 for(int j=0;j<=n;j++){
 if(i==0)
 dp[i][j]=(1);
 else if(j==0)
 dp[i][j]=(2);
 else if((3))
 dp[i][j]=(4);
 else
 dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],(5));
 }
 }
 return dp[m][n];
}
int main(){
 string str1,str2;
 cin>>str1>>str2;
 cout<<"Mininum number of operation:"
 <<edit_dist_dp(str1,str2)<<endl;
 return 0;
}

④处应填（）

dp[i-1][j-1]+1

dp[i-1][j-1]

dp[i-1][j]

dp[i][j-1]

共 3 分　

第42题

#include <iostream>
#include <string>
#include <vector>
using namespace std;
int min(int x,int y,int z){
 return min(min(x,y),z);
}
int edit_dist_dp(string str1,string str2){
 int m=str1.length();
 int n=str2.length();
 vector<vector<int>> dp(m+1,vector<int>(n+1));
 for(int i=0;i<=m;i++){
 for(int j=0;j<=n;j++){
 if(i==0)
 dp[i][j]=(1);
 else if(j==0)
 dp[i][j]=(2);
 else if((3))
 dp[i][j]=(4);
 else
 dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],(5));
 }
 }
 return dp[m][n];
}
int main(){
 string str1,str2;
 cin>>str1>>str2;
 cout<<"Mininum number of operation:"
 <<edit_dist_dp(str1,str2)<<endl;
 return 0;
}

⑤处应填（）

dp[i][j] + 1

dp[i-1][j-1]+1

dp[i-1][j-1]

dp[i][j]

共 3 分　